Colligative Properties: Freezing Point Depression

Introduction

The physical properties of solutions that depend on the number of dissolved solute particles and not their specific type are known as colligative properties. These include freezing point depression, osmotic pressure, and boiling point elevation. In today's experiment you will explore the changes in freezing point behavior of solutions in which t-butyl alcohol (2-methyl-2-propanol) is the solvent.

Freezing point depression occurs when a solute is added to a solvent producing a solution having lower freezing point temperature than the pure solvent. The temperature decreases by an amount ΔT_f given by the following formula:

ΔT_f = K_f c_m

where K_f is the freezing point depression constant (characteristic of the solvent) and c_m is the molal concentration of the solution in moles of solute particles per kilogram of solvent (moles/kg). One way to understand the freezing point depression effect is to consider the solute particles as interfering or standing between the solvent particles. With greater space between solvent particles, intermolecular forces are weaker. Consequently, lower temperatures are required to make it possible for solvent particles to approach each other and form the solid. It is important to note the identity of solute particles isn't specified. That is, an aqueous 0.50 m C₆H₁₂O₆ solution should have the same freezing point as an aqueous 0.25 m NaCl solution, since each formula unit of NaCl provides two ions in solution.

In today's experiment, you will first determine the freezing point of the t-butyl alcohol by cooling it in cold water. You will then add a solute to the alcohol and measure the freezing point of the solution. After determining the freezing point and actual ΔT_f  of the solution, and the masses of solute and solvent, you should be able to determine the K_f of the solvent.

1. Connect a temperature probe to Channel 1 of the LabPro interface and launch the Logger Pro and Excel applications. Set your experiment parameters to the "Time Based" mode, with an experiment length of 10 minutes and a sampling rate of 10 samples/min.

2. Measure and record the mass of a clean, dry large test tube (why is it important for the test tube to be very clean and dry in this lab?) by standing it in a beaker or an Erlenmeyer flask. Using a graduated cylinder, pour 20 mL of t-butyl alcohol into the test tube and measure the new mass. Determine the mass of t-butyl alcohol added. Data that is not collected by Logger Pro should be entered into your laboratory notebook and an Excel spreadsheet.

3. Prepare an ice water bath in a 400-mL beaker. Clamp the test tube to ring stand. Insert a clean, dry copper stirrer into the test tube and clamp a clean, dry temperature probe into the test tube. Make sure that the probe does not touch the walls of the test tube and yet is still well-immersed in the liquid. The copper stirrer should surround the probe.

4. Prepare a warm/hot water bath to warm the liquid in the test tube to a temperature between 40-50°C.

5. When you are ready to begin data collection, click on the "Collect" button. Quickly lower the test tube into the cold water bath (see right). Continuously stir the contents of the test tube with an up/down motion. Make sure the probe remains in the liquid and that it does not come into contact with the walls of the test tube. Stir as long as possible, allowing the data collection to continue until the temperature levels off or a long, gradual slope is obtained (see figures below). Remove the test tube from the cold water bath and place it in a beaker of warm/hot water bath to thaw the solid.

6. Under the Experiment menu, select Store Latest Run. Also, save your file to disk, or to a directory specified by your instructor. Saving early and often prevents any accidental data loss.
       
7. Repeat steps 4-6 so that you have obtained two trials for the pure t-butyl alcohol.
     
8. Remove the test test tube from the clamp and dry it thoroughly. To account for any t-butyl alcohol that may have evaporated or otherwise been lost, measure and record the mass of the test tube and contents on the same balance as before to determine the mass of t-butyl alcohol remaining. Add 1.00-1.50 grams of solute to the t-butyl alcohol. Use a dropper to add a liquid or a spatula to add a solid. Measure and record the precise mass used by reweighing the test tube and contents. Clamp the test tube into place with the clean and dry stirrer and probe assembly. Mix the contents of the test tube thoroughly to ensure the complete dissolution of the solute. Make sure the solute is completely dissolved before proceeding.
     
9. Replace any melted ice in the ice water bath. Then repeat steps 4-6. Repeat steps 4-6 again to obtain two trials for the solution.
     
10. Dispose of the solution in the the designated waste container. Wash and thoroughly dry the test tube, probe, and stirrer.    

Data Analysis

Goal: (1) To determine the freezing point for the pure solvent and for each of two solutions. (2) To use these temperatures to determine the freezing point depression constant, K_f, of the solvent.

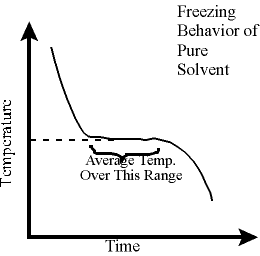
1. As the pure solvent cools, its temperature drops. This is illustrated in the graph to the lower left. During the conversion of liquid to solid, the temperature remains relatively constant and a plateau in the cooling curve is observed. Using your data, use Logger Pro to find the average of the temperatures on the plateau. Record this temperature as the freezing point of t-butyl alcohol.

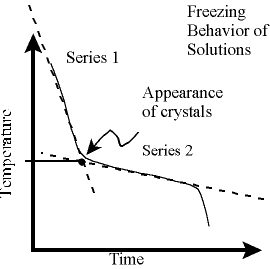
2. The freezing point of a solution is the temperature at which crystals just begin to form. As additional solid forms, the temperature continues to drop. This behavior is illustrated in the graph to the above right. Since the temperature probe is unable to respond instantly to temperature changes, the thermometer records a gradual change in temperature instead of the abrupt change in temperature that should be observed at the instant crystals begin to form. Consequently, the graph is rounded in the vicinity of the appearance of crystals.

   To compensate for the slow response of the thermometer, the solution's freezing point is determined graphically. To do this, you will need to obtain the equations for each of the two "straight-line" series of your solution's cooling curve. The first series includes data obtained as the solution cools and approaches the freezing point. The second series includes data obtained as the solution solidifies. Use Logger Pro to perform a linear regression analysis on each of the two series and determine where the two regression lines intersect. (You may do this by solving the equations of each of the regression lines simultaneously or by substitution, or by zooming in on the intersection of the two lines on the graph). This intersection corresponds to the freezing point of the solution. You will need to perform this type of analysis for each of the solutions in your experiment.

Calculations and Questions

1. Calculate the molality and the freezing point depression for each trial of the solutions.
      
2. Using the molality and the freezing point depressions, calculate the freezing point depression constant for each trial of the solutions. Find the average value for K_f based on your data and submit your average K_f values before leaving the lab (or within 24 hours with instructor approval).
      
3. Gather the all of the K_f values from your lab section and calculate the average value of K_f for t-butyl alcohol.
       
4. Using the class average for K_f and the freezing point of pure t-butyl alcohol determined in the lab, what is the molecular weight of a substance that yields a freezing point of 18.2°C when 1.06 g of the substance was dissolved in 18.36 g of t-butyl alcohol?
      
5. A skyscraper in Pittsburgh, built in the early 1970s is supported by water filled columns. Potassium carbonate was added to the water to prevent freezing during cold weather. If the solution is 40.0% K₂CO₃ by mass, what is the predicted freezing point of this solution in °C, assuming full ionization?
     
6. Melting point temperatures are frequently used to help identify unknown solids and determine their purity. How would the melting point of a pure solid sample compare to that of the same solid contaminated by a solid impurity? Explain.

Lab Report
You may choose to submit an individual or group report for this lab.  Follow the guidelines for Laboratory Reports located at http://webs.anokaramsey.edu/chemistry/Chem1062.  Your report should include a title, procedure, results, and discussion.  Make sure that your graphs include titles, axes labels, regression line equations, trendline equations, etc. Move equation boxes so that they do not cover each other up.  While there are no formal questions for you to answer in the discussion, it should show that you have thought about the data which you have collected and how well you performed the lab overall. The answers to questions three through five should be given in an appendix at the end of the report.

Follow your instructor’s directions for submitting this lab report. Remember to name the file as specified (Lastname_FPDepression or Lastname1_Lastname2_FPDepression). If you are emailing your report, use the subject line “Chem 1062: FP Depression Lab”. If you worked in pairs and are submitting this assignment on an individual basis, please underline your own name and include your lab partner’s name on the assignment. 

Include one set of sample calculations for one of the trials, either handwritten or typed (preferably in Equation 3.0 or a similar program). Alternatively, use an Excel spreadsheet embedded into your Word document if you will be submitting your report electronically to your professor, since your work would be shown in the cell formulae. This will enable the professor to view the formulas in each of your spreadsheet cells rather than having you write them out.

Lab developed by the Anoka-Ramsey Community College Chemistry Department. Portions of this lab were written by Kirk Boraas, Minneapolis Community and Technical College. Last updated April, 2011.